Mathematica

Mathematica · 1月 24日, 2021年

正多面体のグラフィックをやってみたいと思っていたら、共通テストに出たので早速動画を作ってみました。

Mathematica · 12月 20日, 2020年

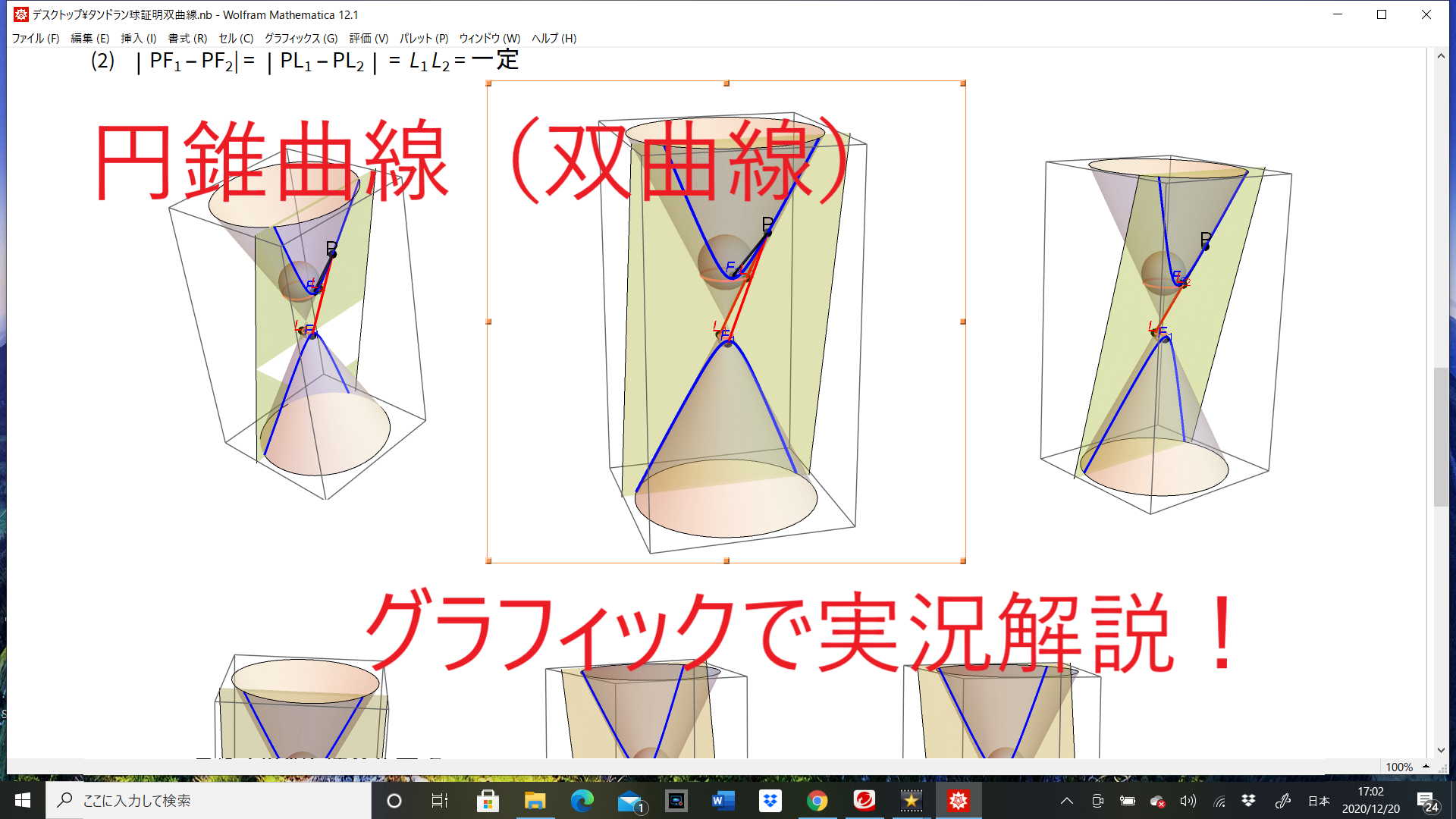
円錐曲線が、楕円、放物線、双曲線になるという証明に Dandelin球 というものが使われます。Mathematica で組み、解説も行いましたので見に来てください。

Mathematica · 12月 13日, 2020年

円錐曲線は、双曲線、放物線、楕円のいずれかであり、焦点は平面と内接球の接点で表されます！これらを具体的に式で表し、グラフィックにしてみます。

Mathematica · 12月 06日, 2020年

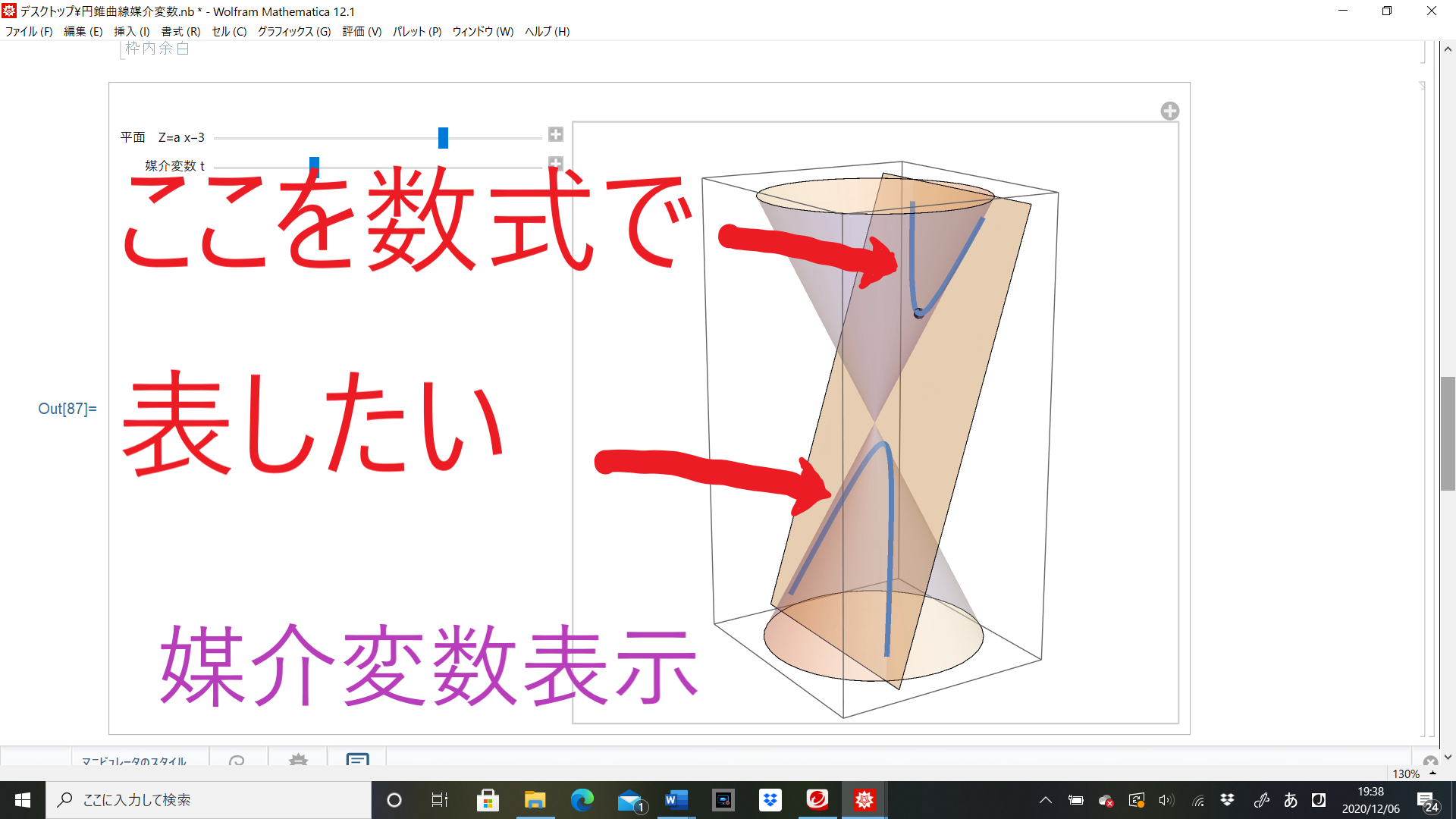
円錐と平面の共通部分（円錐曲線）は、楕円、放物線、双曲線のいずれかになります。この曲面たちを数式で定義し、２次曲線を媒介へ媒介変数で表してみました。

Mathematica · 12月 05日, 2020年

４次関数の２重接線の問題をMathematica で解いてみました。

Mathematica · 11月 29日, 2020年

今まで、任意の２次曲線と言いつつも放物線を除外していました。 今回の notebook は任意の放物線の標準形・焦点・準線・媒介変数表示を求めることができます。

Mathematica · 11月 23日, 2020年

任意の２次曲線を極方程式、極座標表示に変形する（安直な）方法です。 数学Ⅲの教科書に載っています。

Mathematica · 11月 23日, 2020年

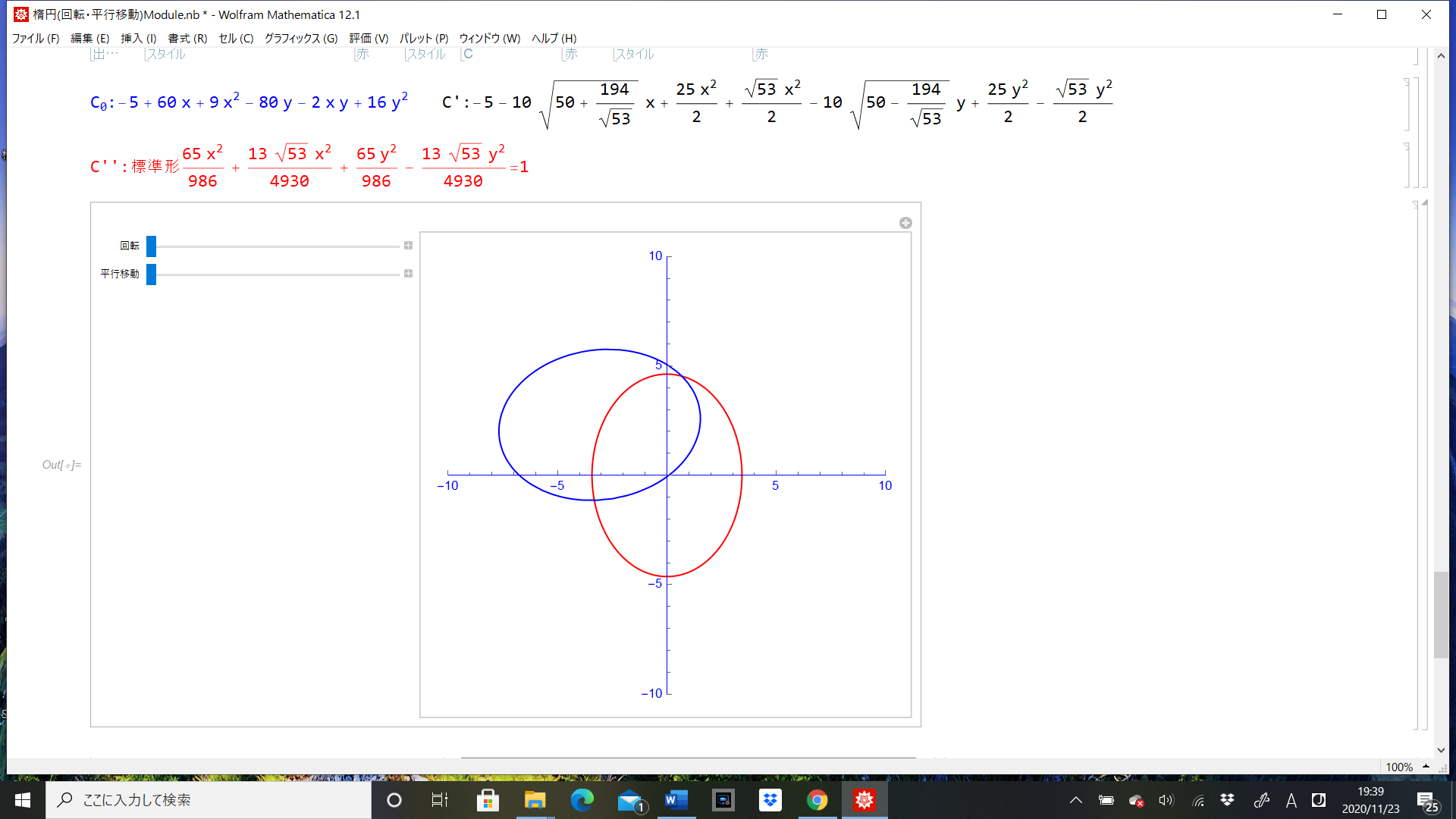
2次曲線を回転、平行移動で標準形に変形する様子を視覚化しました。 実際に動くところを見ると式変形の意味が良く分かります。 ※ファイルダウンロードできます。

Mathematica · 11月 23日, 2020年

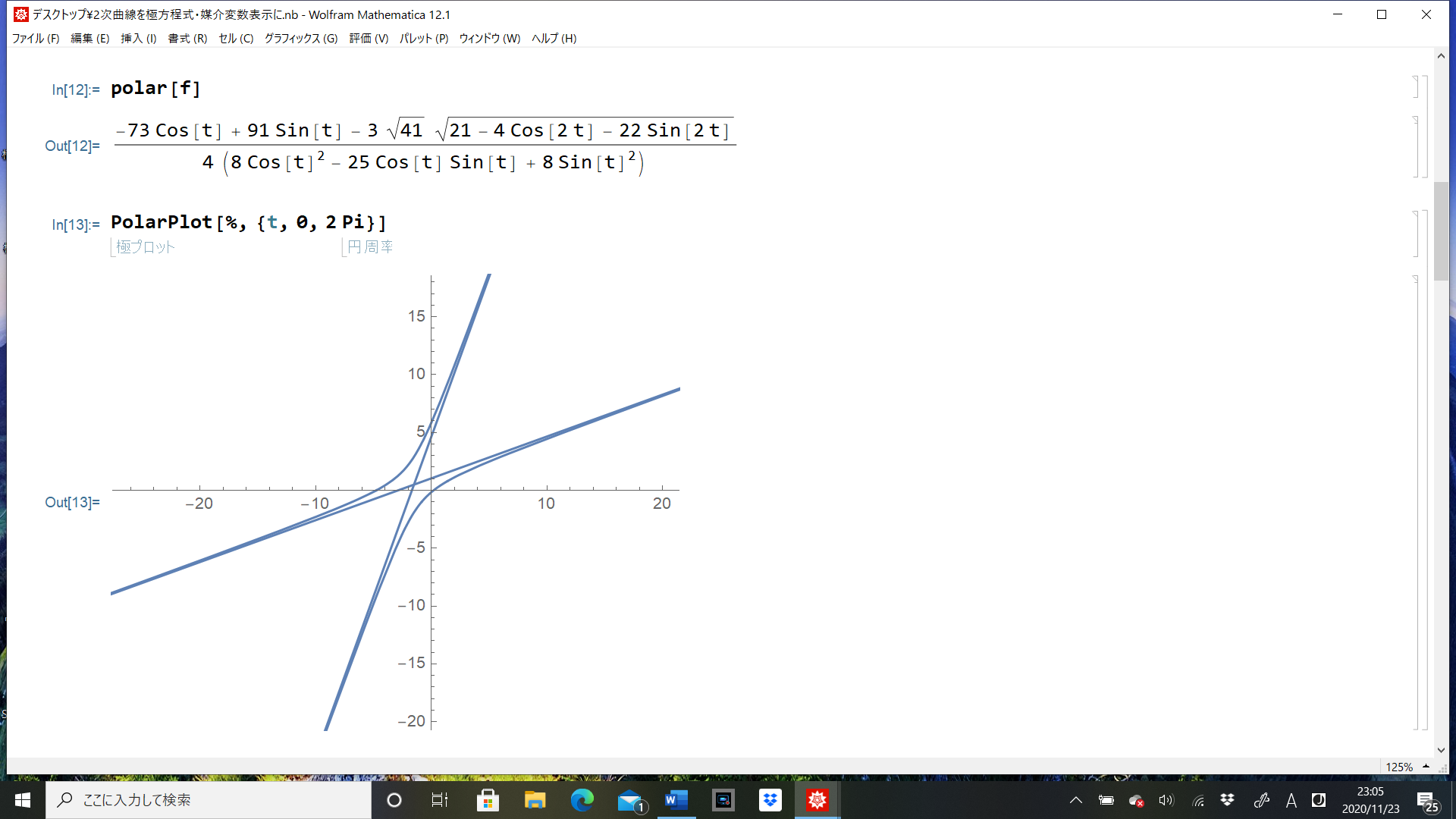
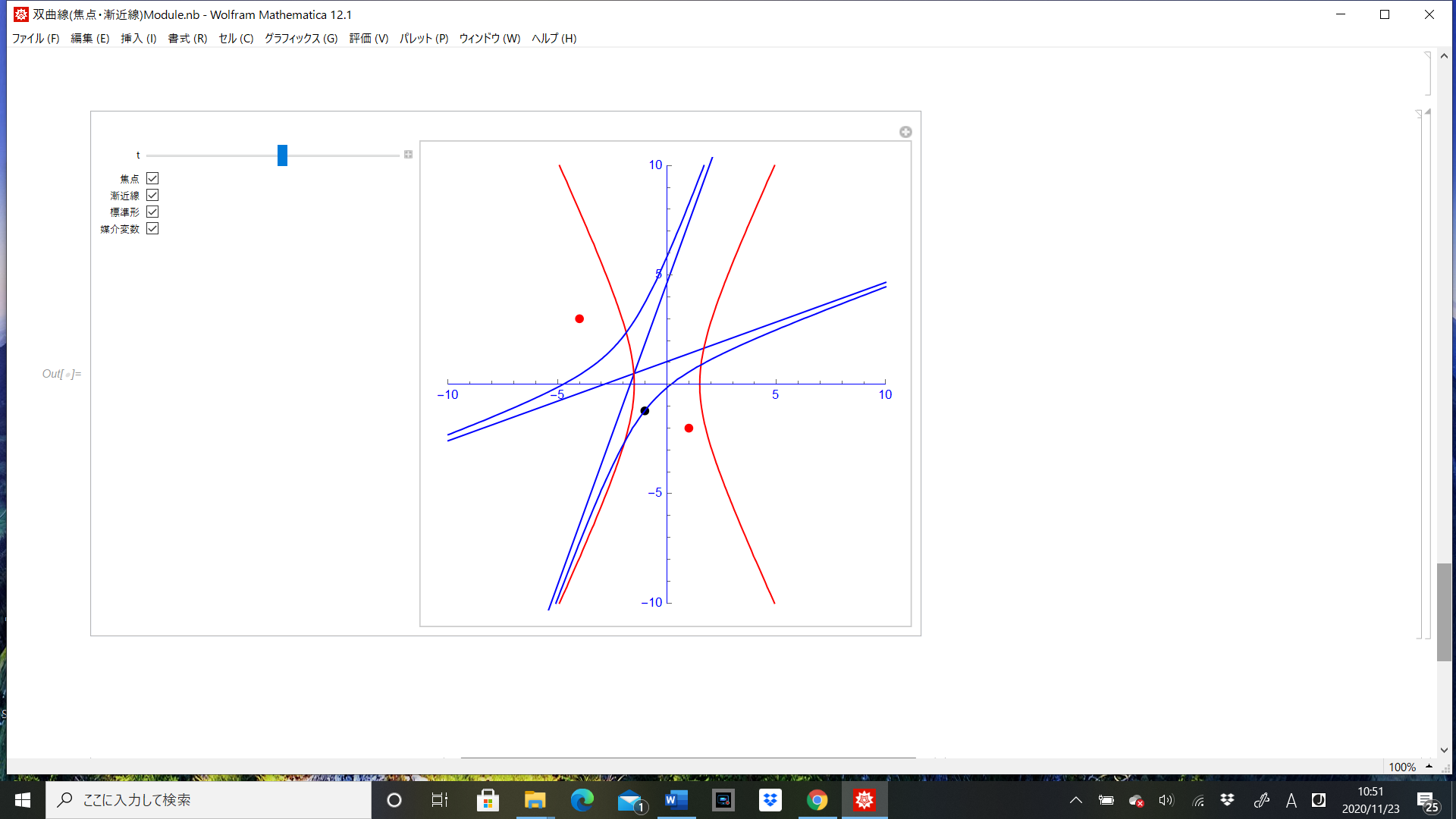
任意の２次関数の焦点、漸近線、媒介変数が求められます。インタラクティブな教材風にしましたので、Mathematicaのインストールされていないパソコンからも操作できます。

Mathematica · 11月 16日, 2020年

任意の２次曲線の媒介変数表示を求めます。Mathematica のファイルは Wolfram Player を用いてインタラクティブに操作できます。